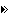【例题】12，25，39，(　　)，67，81，96

A.48　　　　B.54　　　　C.58　　　　D.61

【解析】B。相邻两项之差以13，14，15循环。

【例题】(　　)，11，9，9，8，7，7，5，6

A.10　　　　B.ll　　　　C.12　　　　D.13

【解析】A。奇数项-1为公差，偶数项-2为公差。

【例题】105/60 98/56，91/52，84/48，(　　)，21/12

A.77/42　　　　B.76/44　　　　C.62/36　　　　D.7/4

【解析】D。各项化简后都等7/4。

【例题】某人工作一年的报酬是18000 元和一台洗衣机，他干了7 个月不干了，得到9500元和一台洗衣机，这台洗衣机价值多少钱?

A.8500　　 B.2400 　　C.2000　　 D.1500

【解析】7个月得到9500元和一台洗衣机，所以选项加上9500后能被整除的只有2400， 选B。

【例题】每次加同样多的水，第一次加水浓度15%，第二次加浓度12%，第三次加浓度为多少?

A.8%　　 B.9%　　 C.10%　　 D.11%

【解析】8%跟11%一个相差太大，一个相差太小，排除AD。12%跟15%相差3%，9%也跟12%相差3%，添加后浓度差一定会变，所以排除B，选C。

上面的解法也许有人会认为过于极端，但是不断加水后，浓度差肯定会渐渐变小，另外可以这样解： 因为溶质质量始终不会改变的，所以设盐水有60克的盐(15跟12的最小公倍数) 则第一次加水后溶液是0/0.15=400克，第二次加水后溶液是60/0.12=500克， 所以可知是加了100克水，第三次加水后浓度是60/(500+100)=0.1，也就是10%，选C。

【例题】60 个人里面有12 个人穿白衣服蓝裤子，有34 个人穿黑裤子，有29 人穿黑上衣，求黑裤子黑上衣多少人?

A.13 　　B.14　　 C.15 　　D.20

【解析】直接容斥定理：34+29-(60-12)=15，选C。